x86における
浮動小数点演算の精度の制御と、
80bit 浮動小数点演算問題
update: 2023/NOV/02
初出: 2010/NOV/20
0.はじめのはじめに
みんな大好き Intel x86, AMD 64の浮動小数点演算のアーキテクチャは、
8087時代からの80bit演算に起因し、IEEE 754から逸脱するという欠点があった。
だが、今では、
gcc は、暗黙のうちに、SIMD(SSE,AVXなど)演算器を使用するコードを
生成するようになり、
SIMDユニットにて浮動小数点演算することで、
80bit演算由来の問題が、解消されるようになっている。
ではあるものの、この文書は、延々と80bit起因の問題について述べている。
現在も、8087由来の、x86伝統の内部80bit演算はCPU内には健在である。
80bit演算の害を体験したい場合は、
gccのオプション -mfpmath=387
を指定すればよい。
1.はじめに
様々な機械で、同じ結果を得るために、IEEE 754 (通称 IEEE Float)
が定められている。
現在のほとんどの計算機は IEEE Float準拠である。
しかし、特に x86 で、スパコンや組込みマイコンと同じ結果を得るためには、注意が必要である。
(現在のスパコンの多くが、x86 コアを採用したクラスタ計算機である、などとツッコンではいけない :-P)
x86以外のほとんどの機械は計算を 64bit で行う。
例えば、
スーパコンピュータ、大型機(メインフレーム)、ワークステーション、組込みCPU
ARM,RISC-V, Cray , IBM S/390, PowerStation (PPC), PA-RISC, Sun Sparc, SGI Mips, DEC Alpha など
は、64bitか32bitで演算する。
(Crayの昔のモデルと一部のモデルはIEEE floatではない。S/390は昔はIBM 360式の演算をしていた。現在のzシリーズはIEEE floatが基本)
メジャーな機械では、X86と68000の数値演算コプロセッサである68881,68882だけが 80bit 浮動小数点で演算する。
80bit演算を行っていると内部表現が「豪華」すぎて、油断してプログラミングしていると、他の機械と違う結果が出る。
なんのためにIEEE floatを使っているのか?
どの機械で数値演算を行っても、常に同じ結果が得られる、という安心のために、IEEE Floatが定められている。
※ただし、IEEE 754は、数字の文字列の入出力について規定していない。よって数字の印字形式を読み込んだ時に、
内部でどんな表現になるか、IEEE754形式から印字形式に変換したときに、変換による誤差が生じても、それは野放しである。
UNIX系OSのC言語では、ユーザが精度の制御を行わねばならない。
2. 精度の制御 80bit float問題
x86(と68881,2)だけが 80bit 浮動小数点数で演算する。
でも、
- x86の UNIX, FreeBSD, Linuxは精度の設定ができるよ。
- 例えば、FreeBSD は、丸め設定と同じ風味で設定が可能だ。
- 問題 ないじゃん。
と、思う人が多いだろう。
しかし、それは甘い!
2.1 精度の制御; 80bitモードと64bitモードの切り替え
2.1.1 Linuxの場合
Linuxで、x86の演算モード(演算精度)を切り替えるには、x87制御レジスタのことを知らなければならない。
(下図参照。
図は、
64-ia-32-architectures-software-developer-vol-1-manualより)
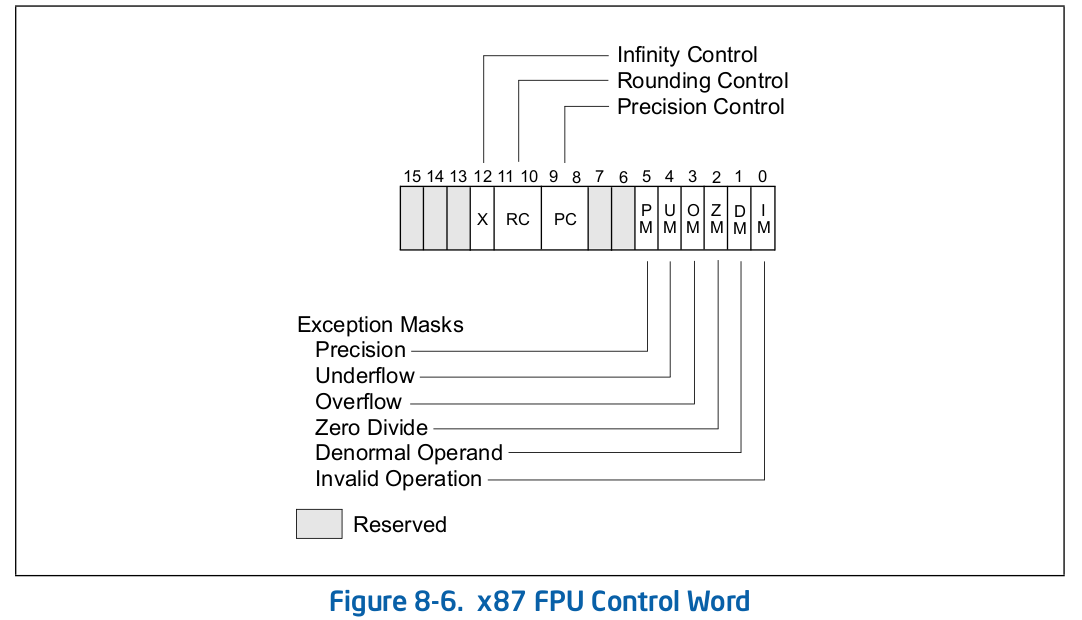

Linuxは、/usr/include/x86_64-linux-gnu/fpu_control.h中に、
下記のような定数があり、
/* precision control */
#define _FPU_EXTENDED 0x300 /* libm requires double extended precision. */
#define _FPU_DOUBLE 0x200
#define _FPU_SINGLE 0x0
それぞれ、_FPU_EXTENDED:80bit、_FPU_DOUBLE:64bit、_FPU_SINGLE:32bit 浮動小数点演算モードの指定である。
Linuxでは、x87浮動小数点演算の精度の設定は、下記のようなコードで行う。
#include <fpu_control.h>
fpu_control_t cw, cwx;
_FPU_GETCW(cw);
cwx= (cw & 0xFCFF)| _FPU_EXTENDED; //80bit
_FPU_SETCW(cwx);
_FPU_GETCW(cw);
printf("cw=0x%x\n", cw);
ちなみに、Linux x86(AMD64)のデフォールトは、_FPU_EXTENDED(80bit)であるが、WSLでは_FPU_DOUBLE(64bit)である。Windowsが_FPU_DOUBLE(64bit)がデフォールトであるためらしい。
なお、Linuxには、
void __setfpucw(unsigned short control_word);
というライブラリ関数があるが、getfpucw()のような、状態を得る関数は無い。
2.1.1 FreeBSDの場合
FreeBSD 13.1R (4.7-STABLE #5から同様)を例にとる。
FreeBSD 13.1R (4.7-STABLE #5から同様)の /usr/include/machine/ieeefp.h 中の構造体
/*
* FP precision modes
*/
typedef enum {
FP_PS=0, /* 24 bit (single-precision) */
FP_PRS, /* reserved */
FP_PD, /* 53 bit (double-precision) */
FP_PE /* 64 bit (extended-precision) */
} fp_prec_t;
それを使用し、Cソースでこんな風に書く
#include <ieeefp.h>
/*#include <machine/floatingpoint.h> FBSD2*/
fpsetprec(FP_PS); /* 32bit指定*/
fpsetprec(FP_PD); /* 64bit指定*/
fpsetprec(FP_PE); /* 80bit指定*/
printf("fpgetprec() = %d\n", fpgetprec()); /* 確認もできる */
この指定方法は、2023年11月現在でも使える。
ただし、今(2023年11月)のclangではdouble であると、正しく64bit演算をしているようだ。
また、long doubleを指定すると、上記のfpsetprec(FP_PD)を行っても、80bit演算されているようである。
2.2 x86で64bit演算指定の無意味さ
2.2.1 x86で64bit演算指定の無意味さの実例
ここでは、x86で、64bit演算指定をしても、効き目が無いことを示す。
非常に小さな数を適当に大きな数で除すると、64bitで表現できないほど小さくなり、精度が落ちる。
したがって、その精度が悪くなった商に、除した数を乗じても、もとの数には戻らない。
ここでは、1.0/1e307 (1.00000000000000010695e-307) を最初に作り、それを
3e16で除したのち、再び3e16を乗じて、もとの1.0/1e307に戻るかを、テストする。
64bit演算では、除算をした時点で精度落ちして、もとの数には戻らない。
80bit演算では、精度落ちせず、もとの数に戻る。
a=1.0/1e307; aはすごく小さな数
printf("a= %25.20e\n", a);
b= a/3e16; aをある数で除して、同じ数を乗ずる
b= b*3e16; aに戻るか? 64bit演算だと戻らなくて正常
printf("b= %25.20e\n", b);
c= a/3e16*3e16; 内部表現が80bitだと戻ってしまう
printf("c= %25.20e\n", c);
このコード断片を実行すると、
内部64bit演算であると、演算誤差により、もとのaに戻らないはずの演算が、
内部80bit演算だと、もとのaに戻ってしまう。
そして、実行結果。
- FP_PE 最適化無し FreeBSD x86 80bit
a= 1.00000000000000010695e-307
b= 1.48219693752373963253e-307
c= 1.00000000000000010695e-307
80bitが精度がいいのはOK
- FP_PD 最適化無し FreeBSD x86 64bit
a= 1.00000000000000010695e-307
b= 1.48219693752373963253e-307
c= 1.00000000000000010695e-307
64bit指定しているのに、80bitと同じ!(どういうこっちゃ)
内部で64bit演算が行われているならば、
本来、cは bと同じ、精度の悪い値になるべき。
- ARM AppleM1 MacBookAir MacOS, ARM RaspberryPi3_modelB Linux,RISC-V Linux, PowerPC G4 MacOSX
a= 1.00000000000000010695e-307
b= 1.48219693752373963253e-307
c= 1.48219693752373963253e-307
内部がいつも64bit演算の機械では、すべて同じ(精度の悪い)結果が得られる。
- 参考:FP_PS 最適化無し FreeBSD x86 32bit(単精度)
a= 1.00000000000000010695e-307
b= 1.48219697792312544166e-307
c= 9.99999959373654373958e-308
単精度なので、めちゃくちゃになって当然。
2.2.2 評価順序の確認
先の例で、 c= a/3e16*3e16; という式が一つに書かれているので、ひょっとすると
評価順序が人間の思いとは別に、乗算を先に行った後、除算を行っているかも知れない。
ここでは、除算が先に行われていることを確認する。
(※ 古いC 言語の文法では、強さが同じ演算子については、ソースコード上の字面とは無関係に、
コンパイラは演算の順序を入れ替えることができる。
加えて言えば、二項演算子の左オペランドと右オペランドのどちらを先に評価するかも、規定されていない。
※Fortranは、浮動小数点演算については、ソースコードの字面の左から右に(人間の習慣にあった)演算を行う。
勝手に演算の順序を入れ替えることはない。整数演算についてはその限りではない。
(参照: 浮動小数点演算の演算順序) )
確認のため、 cc -S seido1.c として、アセンブラのソースを出力させて、それを見る。
fldl -8(%ebp)
fldl .LC4
fdivrp %st,%st(1) b= a/3e16;
fstpl -16(%ebp)
fldl -16(%ebp)
fldl .LC4
fmulp %st,%st(1) b= b*3e16;
:
:
fldl -8(%ebp) c= a/3e16*3e16;
fldl .LC4
fdivrp %st,%st(1)
fldl .LC4
fmulp %st,%st(1)
アセンブリ・ソースで確認できるとおり、fdivrp %st,%st(1) を行った後に、fmulp %st,%st(1) している。
よって、先の精度のテストは、意図したとおりで、問題ない。
ちなみに、このアセンブリ・ソースでは、除算と、乗算を 2行に分けて書いた方は、このように
fstpl -16(%ebp)
fldl -16(%ebp)
浮動小数点数の、メモリへのストアとロードが生成されている。
特に、ストアが生成されていることが重要なのである。(後に詳述)
3. 問題の整理。計算がうまく行く理由
2.2.1のテストにより、
次の2式は、違う結果をもたらすことが分かった。
- b= a/3e16; b= b*3e16;
- b= a/3e16*3e16;
2の式は中間結果が 80bit のまま保持され、また、内部でも80bitで計算が行われる。
結局、64bit指定の意味がまったく無い。
これでは、PowerPCやSPARCと互換性のある計算が行えない。
1の式はどうしてうまく行ったのか?
C言語では、代入は型変換を行う。
今の場合、bという変数への代入が、64bit浮動小数点数への、型変換、すなわち精度の合わせを行う。
機械語命令としては、 fstpl -16(%ebp) が、64bitへの変換を行いつつ、メモリへのストアを行う。
1の式は、一つの演算を行うたびに、64bit変数へのストアを行うので、人間が欲したとおり、64bitの精度で演算を続けることになる。
ということで、
x86 の浮動小数点演算を 64bit で行いたい場合、C言語であれば、
各一演算ごとに一文に分け、各文ごとに、 倍精度変数への格納とする。
(演算を一文ごとに分けるのは、演算の順序を明示的に指定するためでもある。
(参照: 浮動小数点演算の演算順序)) )
基本的には、上は正しい。
しかし、まだまだ、問題がある。
4. 最適化による問題と、その回避
これまでの議論で、変数への格納により、ずっと64bit演算を行わせることができることが分かった。
しかし、伏兵がいる。
完成した数値計算プログラムは例外なく、最適化のオプションを指定するであろう。
それが問題を生む。
先の精度テスト用のコード断片について、最適化の指定をして結果を見る。
- FP_PD 最適化無し
a= 1.00000000000000010695e-307
b= 1.48219693752373963253e-307
c= 1.00000000000000010695e-307
意図どおり
- FP_PD -O4
a= 1.00000000000000010695e-307
b= 1.48219693752373963253e-307
c= 1.48219693752373963253e-307
コンパイル時に静的に最適化され、式は、定数にされてしまっている
このコンパイラでは、コンパイル時計算は、64bit精度で行われているようだ。
- FP_PD -O4 -ffloat-store (正解!)
a= 1.00000000000000010695e-307
b= 1.48219693752373963253e-307
c= 1.00000000000000010695e-307
ロード、ストアが残され、実行時に計算。
- PowerPC G4 MacOSX -O4
a= 1.00000000000000010695e-307
b= 1.48219693752373963253e-307
c= 1.48219693752373963253e-307
PPC 64bitは、いつも64bit
- ※Linux Gcc4では、
-ffloat-storeの効果無し。
-Oと同様の結果
| OS |
コンパイラ |
| FreeBSD 4.7-STABLE #5: i386
|
gcc version 2.95.4 20020320 [FreeBSD]
|
| Darwin Kernel Version 7.9.0: Power Macintosh powerpc
|
gcc version 3.3 20030304 (Apple Computer, Inc. build 1666)
|
| Linux 2.6.11-1.1369_FC4 #1 Thu Jun 2 22:55:56 EDT 2005 i686 i686 i386 GNU/Linux
| gcc 4.0.0 20050519 (Red Hat 4.0.0-8)
|
今回の、OS、コンパイラ
上のテストの2番のように、
-O4 最適化を行うと、変数へのストアが消されてしまい、
64bitへの精度合わせがなくなり、結局80bitで演算が行われてしまう。
これを抑制し、64bitで演算をさせるためのオプションが大抵のコンパイラに
備わっている。
gccでは、 -ffloat-store である。
テストの3番のとおり、 -ffloat-store を指定すれば、最適化を指定しても、意図したとおり、64bitで、演算が行われる。
5. Fortran
数値計算の王道の言語は、Fortranである。
Fortranについても調べた。
結論を言えば、Fortranでも、ストアが行われないと、
64bit 丸めが行われず、80bitで演算が行われてしまう。
5.1 NetBSDの Fortran
なぜか、NetBSDのGnu FortranとMac OS Xの Fortranでテストした。
次のプログラムで、最適化オプションを変えて、テスト。
C 80bit problem
C
implicit real*8 (a-h, o-z)
C
a=1.0/1d307
write(*,*) a
b= a/3d16
b= b*3d16
write(*,*) b
c= a/3d16*3d16
write(*,*) c
stop
end
結果は次のとおり。
- g77 最適化無し
1.E-307
1.48219694E-307
1.E-307
- g77 -O4
1.E-307
1.E-307
1.E-307
最適化で定数にされた
コンパイル時計算も、 64bitではない。
- g77 -O4 -ffloat-store
1.E-307
1.48219694E-307
1.E-307
意図どおり
(最適化なしと同様)
- PowerPC G4 MacOSX -O4
1.E-307
1.48219694E-307
1.48219694E-307
64bitで行われている
| OS |
コンパイラ |
| NetBSD 1.6.1 i386
|
g77 version 2.95.3 20010315 (release) (NetBSD nb3)
|
| Darwin Kernel Version 7.9.0: Power Macintosh powerpc
|
gcc version 3.4 20031015 (experimental)
|
5.2 Intel Fortran
Intel Fortran (Linux下)でも、同様のテストを実施。
- fort -O0 最適化無し
1.000000000000000E-307
1.482196937523740E-307
1.000000000000000E-307
- fort -O4
1.000000000000000E-307
1.482196937523740E-307
1.482196937523740E-307
最適化で定数になっている
- fort -O4 -pc64 -mp1
1.000000000000000E-307
1.482196937523740E-307
1.482196937523740E-307
-mp1はmpより速度影響が少ない
最適化で定数になっている
- fort -O4 -pc64 -mp
1.000000000000000E-307
1.482196937523740E-307
1.000000000000000E-307
-mpは精度厳密で速度遅い
-O0と同様、毎回計算しストア
| OS |
コンパイラ |
| Linux 2.6.11-1.1369_FC4 #1 Thu Jun 2 22:55:56 EDT 2005 i686 i686 i386 GNU/Linux
|
Intel(R) Fortran Compiler for 32-bit applications, Version 9.0 Build 20050430
Z Package ID: l_fc_p_9.0.021
|
6. まとめ
64bit精度で演算をさせるには…
C言語では double 変数,
F77では real*8 変数
が64bit。
浮動小数点演算を行うごとに、その結果をdouble変数に代入すべし。
64bit変数へのストアは精度あわせ(丸め)を、その度に実行する
丸めが、切捨て/切り上げ/四捨五入のいずれであるかは、実行環境に依存する
実行環境とは:IEEE float指定、機械やCコンパイラの限界、プログラマによる明示的指定
また、最適化でストアがなくなってしまうことがありえる。
コンパイラにストア削除を抑制するオプションが用意されている。
X86で、64bit精度の演算を行うには、それらの指定が必須
FORTRANにもストア削除の抑制オプションが存在する場合がある(g77, SunF77)
各コンパイラの、ストア削除の抑制オプション
| gcc, g77
|
-ffloat-store
|
| Sun CC, f77
| -fstore
|
| Intel Fortran
| -pc64 -mp
|
6.1 しかし…
セルフでコンパイルしていても、
コンパイラが最適化時に計算した定数と、
実行時の値が異なるとは!
そもそも
精度の変更が動的にできるということは…
↓
コンパイラで定数の最適化は不可能、もしくは現実的ではないでは?
クロス・コンパイラってしんどそう(ただし、そもそも80bit floatがなければ問題ないよね)
FORTRANのような静的な言語が望まれるなぁ。(80bitのせいで)
ここまで、書いてきたが、首藤さんに、2回丸めが起こり、他の機械と違う
結果が出る場合があることを教えていただいた。
これを回避するには、単純なコンパイルではなく、ちょっとしたコード列を
実行させねばならない。
コンパイラにそういうコードを生成させればよいのだろうが…
この項は、ユーザとしてのお話なので、まぁ、限界があるです。
6.2 80bit問題回避方法
ところで… いまどきの x86 には、SSEとかAVX2 とかがついており…
SSE系演算では、64bit浮動小数点演算はIEEE 64bitで演算が行われる。
「Shohei Yoshida′s Diary」には、それを使用して80bit演算を回避する方法が書いてある。
gccなどには、浮動小数点演算をSSE系演算器で行う指定がある。
gcc -mfpmath=sse
などと、コンパイル時に、オプション指定を行う。
すると、すべての浮動小数点演算が、SSE,AVXなどで実行され、80bit問題から解放される。\(^^)/
たけおか(竹岡尚三)のホームページ

